
This proton removal is not observed in the NMR spectra of any of the mercury reactions. The electrochemistry results, on the same systems, show that the initial reaction involves the removal of the phenoxide protons followed by the resulting catalysis of the mercury species. The mercury( II) ion can cause either (i) the formation of an ion-pair system, which have a characteristic doubling of all signals in the 1H NMR spectrum, (ii) a cleavage reaction to occur resulting in the reformation of the calixarene diester compound 2, but only when the reaction is heated and (iii) “simple” mercury binding to the pyridine rings when the binding studies are carried out using NMR titration techniques. 1H NMR studies showed that the role of solvent, the anion chosen and the initial reaction conditions were critical and that the formation of a “simple” mercury( II) complex was non-trivial. Compared with other PKEET schemes that can be used in trivial solution, our PKEET-PA is more efficient in receivers’ computation and has lower trapdoor size.Mercury ion complexation reactions were carried out between 3 and various mercury( II) salts. Besides, we prove the security of our PKEET-PA scheme against two types of adversaries. We then instantiate the concept to a lightweight PKEET-PA, which achieves constant-size trapdoor. To solve the aforementioned problem, we propose the concept of PKEET supporting partial authentication (PKEET-PA). This will incur storage burden for the tester. The corresponding size of trapdoor in this method is linear with the number of authorized ciphertexts. A trivial solution is authorizing one ciphertext each time and repeating multiple times. It means that the receiver cannot adaptively authorize the test right of any number of ciphertexts to the tester. According to 1 the stability definition of the trivial solution x(/)0 of (5).

However, the tester can only test one ciphertext or all ciphertexts of one receiver with one authorization. of trivial solution x()0 with respect to the vector function h(x) x. In traditional PKEET, the tester is authorized by the data receiver to perform equality test on its ciphertexts. This attribute enables PKEET to be increasingly utilized in cloud storage, where users store their encrypted data on the cloud.

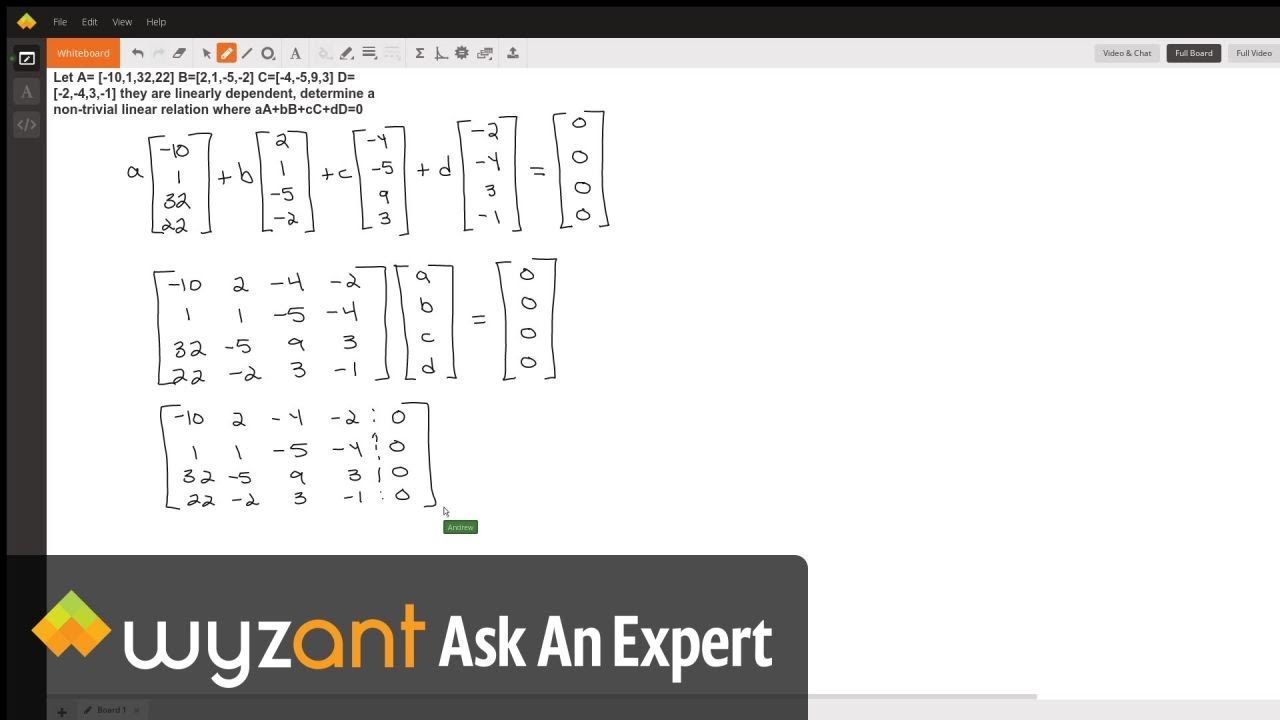
Public key encryption with equality test (PKEET) can check whether two ciphertexts are encrypted from the same message or not without decryption. For the sake of comparison the results obtained from the fourth-order Runge-Kutta numerical method are used to evaluate the presented analytic solutions. For the second problem, we can determine the period and periodic solution in closed-form, which are very accurate. Let us assume that ‘n’ be an integer number. Any other non-zero solution is termed as a non-trivial solution. One simple solution of matrix equation AX O is X 0 which is known as trivial solution. Consequently, after setting the homotopy parameter equal to unity and solving the amplitude equation, the higher order bifurcated solutions can be derived explicitly. In linear algebra, let X be the unknown vector and A is the matrix and O is zero vector.

The constant preceding the displacement is expanded in powers of homotopy parameter and the coefficients are determined to avoid secular solutions appeared in the derived sequence of linear differential equations. To save computational cost and even enhance the accuracy in seeking higher order analytic solutions of these two problems, a modified homotopy perturbation method is invoked after a linearization technique being exerted on the Duffing equation, whose nonlinear cubic term is decomposed at two sides via a weightįactor, such that the Duffing equation is linearized as the Mathieu type differential equation. The second problem is an unconventional periodic problem of Duffing equation in time to determine period and periodic solution. The first problem is the bifurcation of Duffing equation in space, wherein a critical value of the parameter initiates the bifurcation from a trivial solution to a non-trivial solution. In the paper, we solve two nonlinear problems related to the Duffing equations in space and in time.


 0 kommentar(er)
0 kommentar(er)
